Détection d'erreur

Stockage et transmission de l'information

L'information doit souvent être transmise ou stockée:

• envoi d'un mail

• copie d'un texte sur un disque dur externe

• copie d'un film sur une clé USB

• sauvegarde d'un fichier en mémoire

• envoi d'un message via Bluetooth

• envoi d'une photo via Air Drop

• etc.

Lors de ces opérations, il peut y avoir des erreurs.

Erreurs de transmission

Exemple 1

Alice et Bob s'envoient des messages via Bluetooth. Ils se trouvent à une dizaine de mettre l'un de l'autre, la connexion n'est donc pas bonne et le message contient des erreurs.

Bob se rend compte qu'il y a des erreurs dans le message et arrive tout de même à lire et comprendre le message d'Alice.

Lorsque nous transmettons des informations sous forme numérique (suites de 0 et de 1), il y a parfois des erreurs.

Malheureusement, un seul bit peut corrompre tout un fichier. Il est nécessaire de pouvoir garantir l'intégrité des données et donc de détecter et corriger les erreurs.

Principes de base

1. L'émetteur et le récepteur doivent utiliser un ensemble de règles communes.

2. Il faut ajouter ou répéter des informations, c'est-à-dire de la redondance.

Exemple 2

Définitions

Détection d'erreur

Je sais qu'il y a une erreur, mais je ne sais pas où.

Correction d'erreur

Je sais qu'il y a une erreur et je peux la corriger.

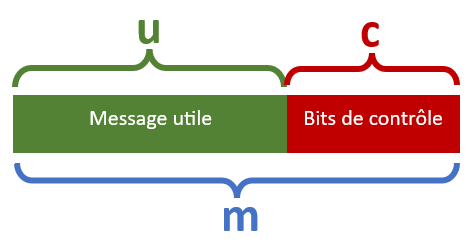
Message utile:

Information que l'on souhaite envoyer. Longueur u bits.

Bits de contrôle:

Bits ajoutés au message utile pour la détection et/ou la correction. Longueur c bits.

Message codé

Message utile auquel on a ajouté de l'information, de la redondance. Message effectivement envoyé. Longueur m = u + c bits.

Code

Transformation d'un message utile en un message codé. Noté: \(X(m, u)\).

Transmission correcte

Lorsque le message décodé est le même que le message utile.
message utile ⇒ message codé ⇒ transmission (avec erreurs) ⇒ message reçu ⇒ message décodé

Exemple 3

L'alphabet IRSA (International Radiotelephony Spelling Alphabet) utilise des mots pour représenter des lettres:

a ⟺ alpha, b ⟺ bravo, c ⟺ charlie, d ⟺ delta, e ⟺ echo, f ⟺ foxtrot, g ⟺ golf, h ⟺hotel, i ⟺ india, j ⟺ juliett, k ⟺ kilo, l ⟺ lima, etc.

Alphabet phonétique de l'OTAN

Capacité de détection C_d

Le code peut toujours détecter C_d erreurs ou moins.

Capacité de correction C_c

Le code peut toujours corriger C_d erreurs ou moins.

Efficacité

L'efficacité d'un code est déterminée par le rapport \(\dfrac{u}{m}\) avec \(\dfrac{u}{m} \leq 1\).

Somme de contrôle (checksum)

Lorsqu'on détecte une erreur, il y a plusieurs possibilités:

• Retransmettre le message

• Corriger l'erreur (processus souvent difficile)

Lors de l'utilisation d'une somme de contrôle, on ajoute au message utile un (ou des) bit(s) de contrôle qui permettent de vérifier selon un certain critère et avec une très haute probabilité que le message reçu est correct.

Bit de parité

Le bit de parité est un exemple de somme de contrôle.
Critère: il doit toujours y avoir un nombre pair de bits 1.

Exemple 4

On veut transmettre un message utile de 4 bits \(B(5, 4)\).
\(u\) = 4 bits, \(c\) = 1 bit et donc \(m = u + c = 4 + 1 = 5\) bits.

message utile	message codé	nombre de bits à 1
0000	00000	0
1011	10111	4
1100	11000	2
0010	00101	2

Capacité de détection:
Avec le bit de parité, on peut détecter un nombre impair d'erreurs. Il n'est pas possible de détecter un nombre pair d'erreurs.

\[C_d = 1\]

Efficacité:

\[\dfrac{u}{m} = \dfrac{4}{5} = 80 \%\]

Exercice 1

On utilise un code \(B(5, 4)\) où on ajoute à un message utile de 4 bits et 1 bit de parité. La somme doit être paire.

Les messages suivants sont-ils corrects?

message reçu	correct?

Exercice 2

On utilise différents codes \(B(n + 1, n)\) où on ajoute à un message utile de \(n\) bits et 1 bit de parité. La somme doit être paire.

Les messages suivants sont-ils corrects?

message reçu	correct?

Exercice 3

On utilise différents codes \(B(n + 1, n)\) où on ajoute à un message utile de \(n\) bits et 1 bit de parité. La somme doit être paire.

Encodez les messages suivants.

message	message encodé

Exercice 4

On considère le code \(B(5, 4)\).

Exercice 5

On ajoute à un message utile de \(n\) chiffres un chiffre de contrôle pour que la somme soit un multiple de 10. Pour chacun des messages suivants, indiquez la somme et déterminez si le message est correct.

message reçu	somme	correct?

Exercice 6

Sachant que le critère pour la somme de contrôle est que la somme doit être un multiple de 10, encodez les messages suivants.

message	message encodé

Exercice 7

La technique de la somme de contrôle permet-elle de détecter:

1. une erreur dans un chiffre?

2. deux erreurs dans deux chiffres?

3. la permutation de deux chiffres?

Solution

1. Oui, une erreur unique est toujours détectée.

2. Pas toujours. Si l'erreur d'un chiffre "compense" celle de l'autre.
   Exemple: 476355 et 872355 ont la même somme de contrôle.

3. Non, une permutation n'est pas détectée.

Algorithme de Luhn

L'algorithme de Luhn est un autre exemple de somme de contrôle. Il consiste à doubler un chiffre sur deux, puis de faire une somme de contrôle sur les chiffres ainsi obtenus (la somme doit être un multiple de 10).

Pour déterminer quels chiffres sont doublés, on part de la fin, et le chiffre de contrôle n'est jamais doublé.

Cet algorithme est notamment utilisé pour valider les numéros de carte de crédit.

Exemple 5

Exemples de décodage

message reçu	message modifié	somme des chiffres	correct?
123789	2267169	2 + 2 + 6 + 7 + 1 + 6 + 9 = 33	non
67892	6148182	6 + 1 + 4 + 8 + 1 + 8 + 2 = 30	oui

Exercice 8

Calculez la somme selon l'algorithme de Luhn des messages suivants et déterminez si le message est correct.

message reçu	somme	correct?

Exercice 9

En utilisant l'algorithme de Luhn, encodez les messages suivants.

message	message encodé

Exercice 10

L'algorithme de Luhn permet-il de détecter:

1. une erreur dans un chiffre?

2. la permutation de deux chiffres consécutifs?

Solution

1. Oui, une erreur unique est toujours détectée.

2. Oui, une permutation de deux chiffres consécutifs est toujours détectée, car l'un est doublé dans la somme, alors que l'autre pas.
   Exemple:
   4713, la somme vaut \(8 + 7 + 2 + 3 = 20\) ⇒ correct
   7413, la somme vaut \(1 + 4 + 4 + 2 + 3 = 14\) ⇒ caux

Exercice 11

Les cartes de crédit suivantes sont-elles valides?

Solution

1. Numéro de carte: 4703 1234 5678 9991
   Numéro modifié: 8703 2264 106148 189181
   Somme: \(8+7+0+3+2+2+6+4+1+0+6+1+4+8+1+8+9+1+8+1 = 80\)
   Ce numéro est correct.

2. Numéro de carte: 4970 1012 3456 7890
   Numéro modifié: 89140 2022 64106 148180
   Somme: \(8+9+1+4+0+2+0+2+2+6+4+1+0+6+1+4+8+1+8+0 = 76\)
   Ce numéro est faux.