Cryptographie asymétrique

Cryptographie asymétrique#

La cryptographie asymétrique, ou cryptographie à clé publique, permet de garantir la confidentialité d'une communication et d'authentifier les participants sans nécessiter le partage préalable d'une clé secrète. Découverts à la fin des années 1960, ces systèmes cryptographiques asymétriques ne présentent pas les faiblesses des systèmes symétriques.

Envoi de message#

Alice souhaite envoyer un message privé à Bob:

  1. Alice écrit son message en clair.

  2. Alice crypte son message avec la clé publique de Bob mise à disposition sur le web.

  3. Alice envoie le cryptogramme à Bob.

  4. Bob déchiffre le cryptogramme à l'aide de sa propre clé privée.

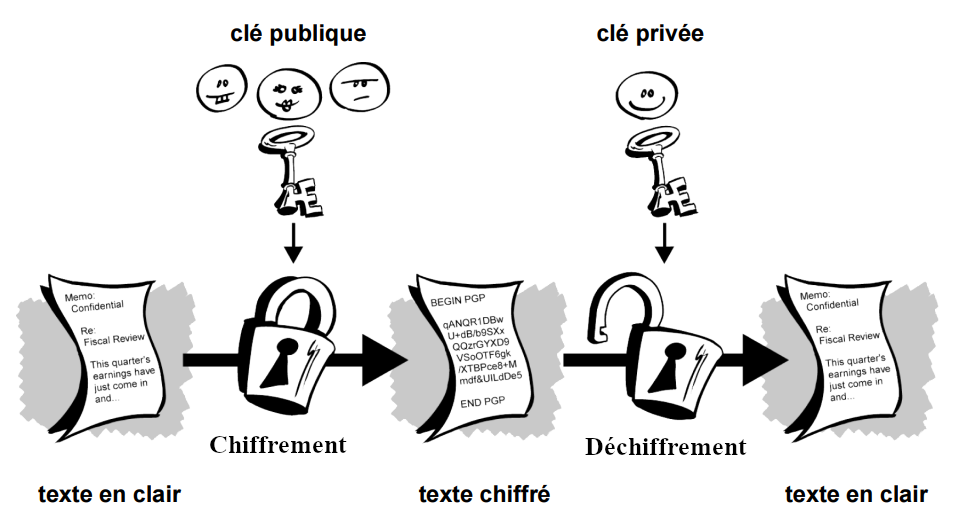
Schéma de la cryptographie asymétrique

source: Network Associates Inc, Introduction à la cryptographie#

Chaque utilisateur possède deux clés:

  • la clé publique qu'il met à disposition sur le web,

  • la clé privée qu'il garde secrète.

Pour déchiffrer un cryptogramme à l'aide d'une clé différente (clé privée) de celle utilisée pour le chiffrer (clé publique), il doit exister une relation entre ces deux clés. Cette relation mathématique est conçue pour empêcher la déduction de la clé privée à partir de la clé publique.

Signature électronique#

Les systèmes à clés publiques ont permis la mise en place de la signature électronique qui garantit l'authenticité d'un message.

Alice souhaite envoyer un message à Bob de telle manière que Bob soir sûr que ce message vient d'Alice:

  1. Alice écrit son message en clair.

  2. Alice crypte son message avec sa clé privée.

  3. Alice envoie le cryptogramme à Bob.

  4. Bob déchiffre le cryptogramme à l'aide de la clé publique d'Alice.

Seule Alice peut signer le message, mais tout le monde est capable de le lire (il n'est pas forcément chiffré).

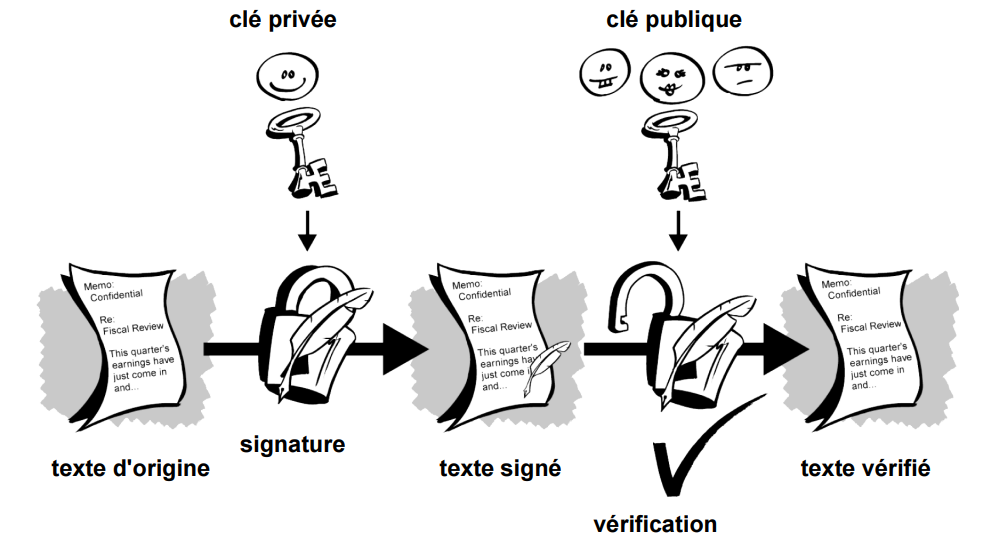
Schéma de la signature électronique

source: Network Associates Inc, Introduction à la cryptographie#

RSA#

Le premier et plus célèbre système cryptographique à clé publique est le système RSA qui sont les initiales de ces trois "inventeurs" (Ronald Riverst, Adi Shamir et Leonard Adleman).

Pour comprendre comment fonctionne le système RSA, nous allons utiliser quelques notions mathématiques de base tels que le reste de la division entière (modulo) et les nombres premiers.

Le modulo est une opération asymétrique, c'est-à-dire qu'il est facile de calculer \(c\) tel que \(c\) = \(a \textrm{ mod } b\) (\(a\) et \(b\) sont connus). Cependant, il est impossible de retrouver \(a\), si \(b\) et \(c\) sont donnés.

Exemple:
\(a \textrm{ mod 5 } = 3\) (le reste de la division de \(a\) par 5 vaut 3)
\(a\) peut valoir 3, 8, 103, 68, ...

Certaines opérations sont faciles, tel que multiplier deux nombres premiers.
Que vaut \(17 \cdot 241\)?

Certaines opérations sont difficiles, tel que factoriser un nombre en facteurs premiers.
Quels sont les facteurs de 4097?

Le système RSA repose sur la capacité à déchiffrer le cryptogramme malgré l'utilisation d'un modulo, en tirant parti des propriétés des nombres premiers. Il s'appuie sur la difficulté à factoriser un nombre en facteurs premiers.

Création des clés#

Méthode#

Pour que le chiffrement RSA soit sûr, il faut utiliser des clés de taille suffisamment grande. Les nombres choisis devront avoir plus de 100 chiffres.

  1. Choisir deux nombres premiers \(p\) et \(q\).

  2. Calculer \(n = p \cdot q\).

  3. Calculer \(\phi = (p - 1) \cdot (q - 1)\).

  4. Choisir un nombre premier \(e\) tel que \(\phi \textrm{ mod } e \ne 0\).

  5. Rechercher \(d\), \(d \ne e\) tel que \((e \cdot d) \textrm{ mod } \phi = 1\).

La clé publique sera composée des nombres \(n\) et \(e\), notée (\(n\), \(e\)).

La clé privée sera composée des nombres \(p\), \(q\) et \(d\), notée (\(p\), \(q\), \(d\)).

Exemple#

Alice souhaite générer sa clé privée et sa clé publique pour pouvoir échanger des messages en toute sécurité avec Bob.

  1. Alice choisit \(p = 5\) et \(q = 11\).

  2. Alice calcule \(n = p \cdot q = 5 \cdot 11 = 55\).

  3. Alice calcule \(\phi = (p - 1) \cdot (q - 1) = 4 \cdot 10 = 40\).

  4. Alice choisit \(e = 43\), car \(40 \textrm{ mod } 43 = 40 \ne 0\).

  5. Alice cherche \(d\), \(d \ne 43\) tel que \((43 \cdot d) \textrm{ mod } 40 = 1\).
    Essais:
    \(d = 3 \quad \quad (43 \cdot 3) \textrm{ mod } 40 = 129 \textrm{ mod } 40 = 9 \;\, \quad \quad\) ❌
    \(d = 4 \quad \quad (43 \cdot 4) \textrm{ mod } 40 = 172 \textrm{ mod } 40 = 12 \quad \quad\) ❌
    \(d = 5 \quad \quad (43 \cdot 5) \textrm{ mod } 40 = 215 \textrm{ mod } 40 = 15 \quad \quad\) ❌
    \(d = 6 \quad \quad (43 \cdot 6) \textrm{ mod } 40 = 258 \textrm{ mod } 40 = 18 \quad \quad\) ❌
    \(d = \dots \)
    \(d = 27 \quad \;\, (43 \cdot 27) \textrm{ mod } 40 = 1161 \textrm{ mod } 40 = 1 \quad \;\,\) ✅

  6. Alice garde secret sa clé privée (5, 11, 27) et publie sa clé publique (55, 43).

Exercice 5#

Déterminer la clé publique et la clé privée du système RSA avec les deux nombres premiers suivants:
\(p = 13\) et \(q = 11\).

Astuce

Utiliser WolframAlpha comme aide pour les calculs.

Solution

  1. Calculer \(n = p \cdot q = 13 \cdot 11 = 143\).

  2. Calculer \(\phi = (p - 1) \cdot (q - 1) = 12 \cdot 10 = 120\).

  3. Choisir e, tel que \(120 \textrm{ mod } e \ne 0\) et e premier.
    Choisissons \(e = 7\), car \(e\) n'est pas un divisieur de 120.

  4. En utilisant WolframAlpha, il faut résoudre l'équation: \((7 \cdot d) \textrm{ mod } 120 = 1\).
    On obtient \(d = 120 \cdot m + 103\) avec \(m \in {Z}\).
    Choisissons \(d = 103\) (\(m = 0\)).

La clé privée est (13, 11, 103) et la clé publique est (143, 7).

Chiffrement#

Méthode#

  1. Chercher dans l'annuaire la clé publique du destinataire de la forme (\(n\), \(e\)).

  2. Transformer le message (texte clair) en nombre, en remplaçant chaque lettre par son code ASCII étendu. A -> 65, B -> 66, a -> 97, etc. Le message est donc maintenant un nombre.

  3. Si le nombre ainsi obtenu est plus grand que \(n\), découper le message en blocs de taille \(m\) tel que \(1 < m < n\). Ces blocs seront chiffrés et envoyés séparément.

  4. Le cryptogramme correspond au nombre \(c\) calculé en utilisant \(c = m^e \textrm{ mod } n\).

Exemple#

Pour simplifier l'exemple, nous remplaceront chaque lettre par son rang dans l'alphabet, plutôt que par son code ASCII étendu.

Bob souhaite envoyer à Alice le message suivant: "salut".

  1. Bob cherche dans l'annuaire la clé publique d'Alice qui est (55, 43).

  2. Bob transforme le message en nombre: s -> 19, a -> 01, l -> 12, u -> 21, t -> 20.
    Le message transformé donnera: 19 01 12 21 20.

  3. Comme 1901122120 > 55, Bob décide de découper en blocs d'une lettre (toujours inférieur ou égal à 26, donc forcément < 55).
    Il y aura donc 5 blocs qui seront chiffrés et envoyés séparément.

  4. Bob détermine le cryptogramme de chaque bloc, noté \(m\), en utilisant la formule suivante:

    \[c = m^{43} \textrm{ mod } 55\]
    s: \(c = 19^{43} \textrm{ mod } 55 = 39\)
    a: \(c = 1^{43} \textrm{ mod } 55 = 1\)
    l: \(c = 12^{43} \textrm{ mod } 55 = 23\)
    u: \(c = 21^{43} \textrm{ mod } 55 = 21\)
    t: \(c = 20^{43} \textrm{ mod } 55 = 25\)

    Bob transmet à Alice le cryptogramme suivant composé de 5 blocs: 39 01 23 21 25.

Exercice 6#

Chiffrer le message \(m = 34\) à l'aide du système RSA, avec la clé publique (143, 7).

Solution

  1. \(n = 143\) et \(e = 7\)

  2. \(34 < 143\) , donc pas besoin découper le message.

  3. Chiffrer le message: \(c = 34^{7} \textrm{ mod } 143 = 122\).

Le message chiffré est 122.

Déchiffrement#

Méthode#

  1. Utiliser la clé privée (\(p\), \(q\), \(d\)).

  2. Déchiffrer chacun des blocs reçus avec la formule suivante: \( m = c^d \textrm{ mod } n \).

  3. Transformer le nombre en lettre, c'est-à-dire remplacer chaque code ASCII étendu par la lettre correspondante.

Exemple#

Alice a reçu le cryptogramme suivant composé de 5 blocs: 39 01 23 21 25.

  1. Alice reprend sa clé privé (5, 11, 27).

  2. Alice déchiffre chaque bloc, noté c, avec la formule suivante: \( m = c^{27} \textrm{ mod } (5 \cdot 11) = c^{27} \textrm{ mod } 55\).
    39: \(m = 39^{27} \textrm{ mod } 55 = 19\)
    01: \(m = 1^{27} \textrm{ mod } 55 = 1\)
    23: \(m = 23^{27} \textrm{ mod } 55 = 12\)
    21: \(m = 21^{27} \textrm{ mod } 55 = 21\)
    25: \(m = 25^{27} \textrm{ mod } 55 = 20\)

  3. Alice transforme le nombre en lettre (pour faciliter, nous avions pris le rang de la lettre dans l'alphabet au lieu du code ASCII étendu): 19 -> s, 1 -> a, 12 -> l, 21 -> u et 20 -> t.
    Le message reçu est donc "salut".

Exercice 7#

Vous avez reçu un message chiffré \(c = 122\).
Déchiffrer le message \(m\) sachant que votre clé privée est (13, 11, 103).

Solution

  1. La clé privée est (13, 11, 103).

  2. Déchiffrer le message: \(m = 122^{103} \textrm{ mod } (13 \cdot 11) = 34\).

Le message clair est 34.

Conclusion#

Le chiffrement asymétrique est plus lent, mais offre une sécurité renforcée. En revanche, le chiffrement symétrique est rapide, mais il est vulnérable aux interceptions et nécessite une distribution sécurisée des clés. Ces deux techniques présentent des avantages et des inconvénients et sont souvent utilisées conjointement:

  • Échange d'une clé symétrique en utilisant la cryptographie asymétrique.

  • Transmission des messages en utilisant la clé symétrique échangée et un algorithme de chiffrement symétrique.

Pour s'assurer que la clé publique appartient bien à la personne concernée, on peut:

  • Se rencontrer physique pour faire l'échange.

  • Passer par une autorité de certification qui contrôle l'identité de la personne et stocke la clé (par exemple DigiCert).

Résumé en vidéo#