Correction d'erreur#
Introduction#
Dans le chapitre précédent, nous avons vu des procédés qui permettent de détecter des erreurs. Lorsqu'une erreur est détectée, nous aimerions dans l'idéal la corriger. Mais la correction est une opération compliquée et elle n'est dans certains cas pas nécessaire.
Exemple 6#
Carte de crédit#
Lorsqu'un numéro de carte de crédit est entré sur un site web, un code détecteur d'erreur permet de savoir si le numéro est correct ou pas. Dans ce cas, seule l'information de la validité du numéro est intéressante.
Connexion téléphonique#
Lors d'un appel téléphonique, des erreurs peuvent se produire. Comme la communication est synchrone, il n'est pas possible d'utiliser un code correcteur d'erreur, mais le code détecteur d'erreur permet simplement d'ignorer la partie du message qui contient une erreur et la conversation est tout de même compréhensible.
Transmission entre Mars et la Terre#
Lorsqu'une sonde qui se trouve sur Mars envoie un message, la latence (le délai de transmission) peut être plus de 22 minutes. Dans ce cas, le renvoi du message n'est pas une solution.
Sauvegarde de données sur un disque dur externe#
Lorsqu'une erreur est détectée lors de la copie de données sur un disque dur externe, il est facile de retransmettre les données. Cela est plus rapide que d'utiliser un code correcteur d'erreur.
Codes correcteurs d'erreur#
Les exemples précédents montrent qu'il n'est souvent pas nécessaire de corriger des erreurs et que le simple fait de savoir est suffisant. Mais dans certains cas, il est essentiel de pouvoir corriger des erreurs.
Nous allons voir deux procédés qui permettent de corriger des erreurs.
Répétition de l'information#
Chaque bit est répété \(n\) fois.
Exemple 7#
\(H(3, 1)\)
message utile |
message codé |
|---|---|
0 |
000 |
1 |
111 |
message utile: 0 -> message codé (envoyé): 000
message reçu |
nombre d'erreurs |
message décodé |
correct? |
|---|---|---|---|
000 |
0 |
0 |
oui |
001 |
1 |
0 |
oui |
010 |
1 |
0 |
oui |
100 |
1 |
0 |
oui |
110 |
2 |
1 |
non |
101 |
2 |
1 |
non |
011 |
2 |
1 |
non |
111 |
3 |
1 |
non |
Une erreur est détectée et corrigée.
Deux erreurs sont détectées, mais mal corrigées.
Trois erreurs ne sont pas détectées.
\(C_d = 2\) et \(C_c = 1\)
Efficacité: u = 1 et m = 3
\(\dfrac{u}{m} = \dfrac{1}{3} \cong 33.3 \%\)
Exercice 12#
En vous aidant de l'exemple précédent, effectuez la même analyse du code \(H(3, 1)\) pour le message utile: 1.
Solution
message utile: 1 -> message codé (envoyé): 111
message reçu |
nombre d'erreurs |
message décodé |
correct? |
|---|---|---|---|
111 |
0 |
1 |
oui |
110 |
1 |
1 |
oui |
101 |
1 |
1 |
oui |
011 |
1 |
1 |
oui |
001 |
2 |
0 |
non |
010 |
2 |
0 |
non |
100 |
2 |
0 |
non |
000 |
3 |
0 |
non |
L'efficacté, la capacité de détection et la capacité de correction sont les mêmes, car elles ne dépendent pas du message envoyé, mais du code utilisé, ici \(H(3, 1)\):
\(C_d = 2\) et \(C_c = 1\)
Efficacité \(\cong 33.3 \%\)
Code de Hamming#
Le code de correction d'erreur le plus efficace est le code de Hamming. Il utilise plusieurs bits de parité sur des morceaux différents.
Structure du code de Hamming \(H(m, u)\):
Il est composé de différents éléments:
le message utile composé de \(u\) bits
les \(c\) bits de contrôle de parité
Les \(u\) bits du message et les \(c\) bits de contrôle sont mélangés, mais placés à des endroits bien définis.
Le message codé est de longueur \(m = 2^u - 1\), C'est-à-dire 7, 15, 31, ...
Les bits de parité \(p_i\) sont en position \(2^i\), avec \(i = 0, 1, 2, \dots\)
Les bits du message \(d_i\) occupent les autres places.
Exemple 8#
\(H(7, 4)\)
Message utile de 4 bits: \(d_1\), \(d_2\), \(d_3\) et \(d_4\)
Bits de contrôle: il y a 3 bits de parité \(p_1\), \(p_2\) et \(p_3\)
Les bits de données vont dans un ordre particulier:
|
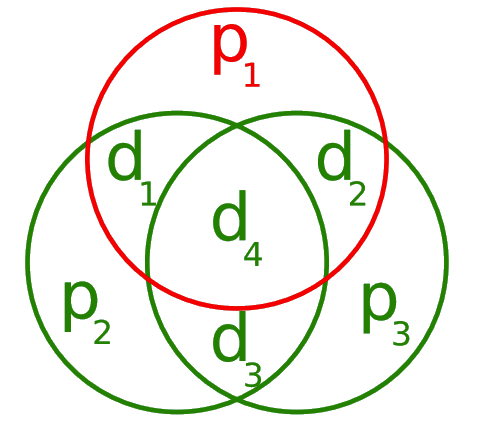
\(p_1\): bit de parité de \(d_1\), \(d_2\) et \(d_4\) \(p_2\): bit de parité de \(d_1\), \(d_3\) et \(d_4\) \(p_3\): bit de parité de \(d_2\), \(d_3\) et \(d_4\) |
|
Vérification: Les trois parités doivent être correctes.
Cas 1: une parité fausse#
|
Parité 1: \(p_1\), \(d_1\), \(d_2\), \(d_4\) ✗ Parité 2: \(p_2\), \(d_1\), \(d_3\), \(d_4\) ✓ Parité 3: \(p_3\), \(d_2\), \(d_3\), \(d_4\) ✓ => \(p_1\) est faux |
|
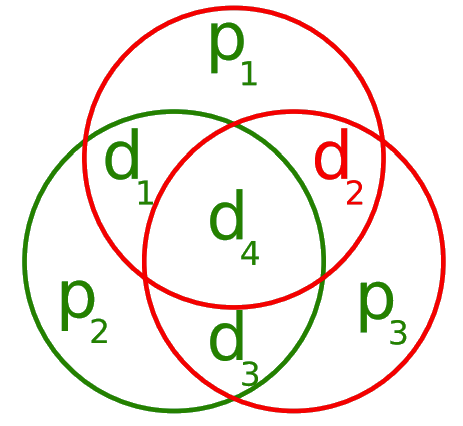
Cas 2: deux parités fausses#
|
Parité 1: \(p_1\), \(d_1\), \(d_2\), \(d_4\) ✗ Parité 2: \(p_2\), \(d_1\), \(d_3\), \(d_4\) ✓ Parité 3: \(p_3\), \(d_2\), \(d_3\), \(d_4\) ✗ => \(d_2\) est faux |
|
Cas 3: trois parités fausses#
|
Parité 1: \(p_1\), \(d_1\), \(d_2\), \(d_4\) ✗ Parité 2: \(p_2\), \(d_1\), \(d_3\), \(d_4\) ✗ Parité 3: \(p_3\), \(d_2\), \(d_3\), \(d_4\) ✗ => \(d_4\) est faux |
|
Vérification des trois parités:
Une erreur est détectée et corrigée.
Deux erreurs sont détectées, mais mal corrigées.
Trois erreurs ne sont pas détectées.
\(C_d = 2\) et \(C_c = 1\)
Efficacité: u = 4 et m = 7
\(\dfrac{u}{m} = \dfrac{4}{7} \cong 57.1 \%\)
Exercice 13#
On considère le code de Hamming \(H(7, 4)\). Pour chacun des messages utiles suivants:
indiquez les 3 bits de parités
encodez le message
message utile |
\(p_1\) |
\(p_2\) |
\(p_3\) |
message codé |
|---|---|---|---|---|
1010 |
1 |
0 |
1 |
1011010 |
Exercice 14#
On considère le code de Hamming \(H(7, 4)\). Pour chacun des messages reçus suivants:
indiquez si chacune des 3 parités est correcte ou fausse
indiquez quel bit est erroné (laissez vide s'il n'y en a pas)
corrigez le message reçu
décodez le message
message reçu |
parité 1 |
parité 2 |
parité 3 |
bit erroné |
message corrigé |
message décodé |
|---|---|---|---|---|---|---|
0101001 |
fausse |
correcte |
correcte |
1 |
1101001 |
0001 |