Cryptographie symétrique

La cryptographie symétrique, également appelée cryptographie à clé secrète, est la méthode de chiffrement la plus ancienne. Elle repose sur l'utilisation d'une même clé pour chiffrer et déchiffrer un message.

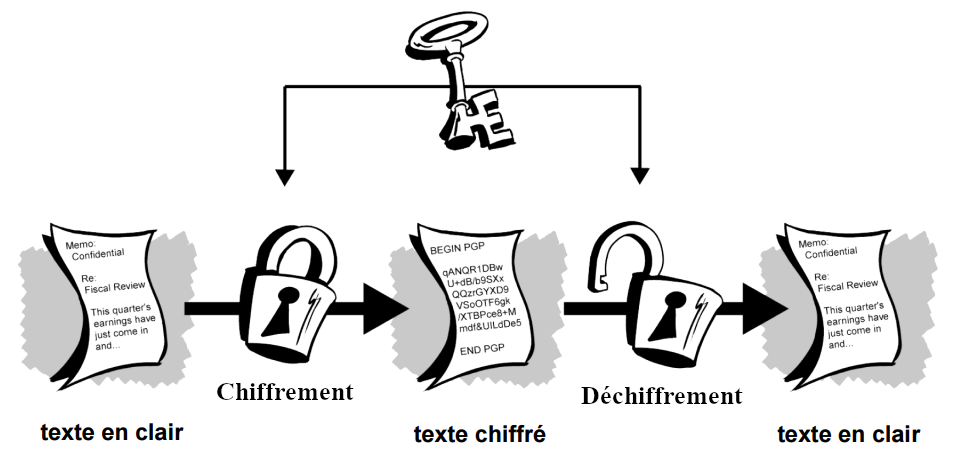
source: Network Associates Inc, Introduction à la cryptographie

• Une clé est choisie et échangée entre les participants.

• Le chiffrement et le déchiffrement s'effectue à l'aide d'un algorithme qui utilise cette clé.

Transpositions

Dans une transposition, les lettres du texte clair sont mélangées, mais pas modifiées. C'est-à-dire que le texte mélangé est une anagramme du texte d'origine.

Scytale

Ce procédé était déjà utilisé pendant l'Antiquité par les Spartes. La scytale est un morceau de bois autour duquel est entouré une bande de cuir ou de parchemin. L'expéditeur écrit son message et déroule la bande qui est une suite de lettre sans signification. Le messager amène cette bande, en générale portée comme ceinture, au destinataire qui enroulera cette bande sur son bâton de même diamètre pour lire le message en clair. Clé de chiffrement: la largeur du bâton.

source: apprendre en ligne

Chiffre Rail Fence

Ce procédé a été beaucoup utilisé pendant la guerre de Sécession. Le Rail Fence dispose les lettres en "zig-zag" sur un nombre de lignes donné.

Le texte "vive le collège saint-croix" donnera le message codé sur 2 lignes: VVLCLEEANERIIEEOLGSITCOX
Écrit en "zig-zag", cela donne:

V V L C L E E A N E R I
 I E E O L G S I T C O X

Le même texte donnera le message codé sur 3 lignes: VLLENRIEEOLGSITCOXVCEAEI
Écrit en "zig-zag", cela donne:

V   L   L   E   N   R
 I E E O L G S I T C O X
  V   C   E   A   E   I

Clé de chiffrement: le nombre de lignes.

Exercice 1

Un texte a été chiffré avec le procédé du Chiffre de Rail Fence avec comme clé de chiffrement 2.
Déchiffrer le texte suivant:

LCYTG AHEYE RQESF CLAEH FRRAR PORPI SMTIU ETAIE DCIFE

Solution

Il y 45 caractères \(45 : 2 = 22.5\). Il y aura 23 caractères sur la première ligne et 22 sur la deuxième.

L C Y T G A H E Y E R Q E S F C L A E H F R R
 A R P O R P I S M T I U E T A I E D C I F E

la cryptographie symetrique est facile a dechiffrer

Substitutions monoalphabétiques

Dans une substitution monoalphabétique, aussi appelée substitution simple, chaque lettre est remplacée par un autre symbole, toujours le même.

Chiffre de César

Ce procédé, déjà utilisé dans l'Antiquité, était connu des Romains. Jules César, dont elle tire le nom, l'employait pour chiffrer certaines de ses correspondances. La substitution proposée par César est un décalage de trois positions. C'est-à-dire que le a est remplacé par D, b par E, etc.

Clair	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
Chiffré	D	E	F	G	H	I	J	K	L	M	N	O	P	Q	R	S	T	U	V	W	X	Y	Z	A	B	C

Clé de chiffrement: décalage de trois positions.

Exercice 2

Coder le message suivant en utilisant le chiffre de César d'origine (décalage de trois positions):

La crypto, c'est sympa!

Solution

Il faut effectuer un décalage de 3 positions pour chaque lettre:
l -> O, a -> D, c -> F, ...

ODFUB SWRFH VWVBP SD

Exercice 3

Déchiffrer le texte suivant chiffré en utilisant le Chiffre de César d'origine, c'est-à-dire avec comme clé de chiffrement un décalage de trois positions.

WHAWH FRGHD YHFOH FKLII UHGHF HVDU

Solution

Un décalage de 3 positions vers la droite a été utilisé pour coder, il faut donc faire une décalage vers la gauche de 3 positions pour décoder:
W -> t, H -> e, A -> x, ...

texte code avec le chiffre de cesar

Remarque

Comme il y a 26 lettres de l'alphabet, il est possible de décaler de 1 à 25 positions. Il existe donc 25 clés de César différentes.

Une telle substitution n'est pas très sûre, car la connaissance d'une seule lettre permet de découvrir tout le message sans difficulté.

Si les 25 positions possibles sont testées, le message sera découvert.

Cas général

Pour rendre le décryptage plus difficile, on peut substituer à chaque lettre une lettre tirée au hasard. Dans ce cas, il y a environ \(1.5 \cdot 10^{25}\) possibilités.

Clair	a	b	c	d	e	f	g	h	i	j	k	l	m	n	o	p	q	r	s	t	u	v	w	x	y	z
Chiffré	K	T	E	W	Q	J	S	V	M	A	Z	G	P	X	C	U	I	O	B	L	Y	F	R	N	D	H

Clé de chiffrement: le tableau de correspondance entier.

Attaque

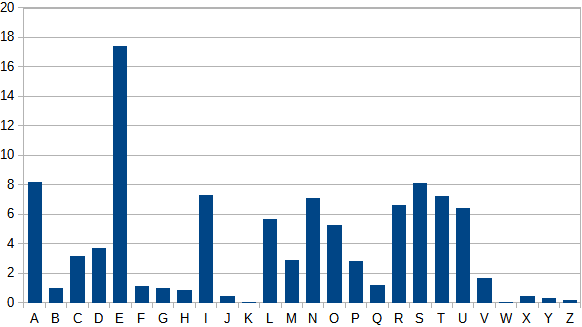
Une méthode efficace pour attaquer un message qui utilise une substitution monoalphabétique est l'analyse des fréquences. En supposant que le symbole le plus fréquent remplace la lettre la plus fréquente en français (le "e") et en appliquant cette logique aux autres lettres, il devient possible de décrypte le message, à condition qu'il soit suffisamment long.

Voici un tableau qui représente la fréquence d'apparition des lettres en français (les lettres accentuées ont été remplacée par des lettres non accentuées, les espaces et ponctuations ont été supprimés).

Lettre	e	a	s	i	t	n	r	...
Fréquence (en %)	17.4	8.2	8.1	7.3	7.2	7.1	6.6	...

source: apprendre en ligne

Substitutions polyalphabétiques

Dans une substitution polyalphabétique, une lettre dans le texte clair peut être remplacée par différents symboles dans le cryptogramme.

Ce procédé rend le décryptage beaucoup plus difficile, car l'analyse de fréquences vue précédemment ne peut pas être utilisée.

Chiffre de Vigenère

Blaise Vigenère (1523-1596) est un diplomate, cryptologue, kabbaliste, traducteur, alchimiste et astrologue français. S'appuyant sur les travaux de ses prédécesseurs (Alberti, Trithème, Bellaso et Porta), il a mis au point le chiffre qui porte désormais son nom.

Le chiffre de Vigenère est une amélioration du chiffre de César. Il utilise 26 alphabets décalés pour chiffrer un message.

Clé de chiffrement: un mot choisi.

Chiffrons "tout est perdu" avec comme clé CRYPTO.

1. Écrire la clé en la répétant pour qu'elle soit de même longueur que le texte en clair.

2. Calculer le décalage pour chaque lettre de la clé. A->C: décalage de 2 positions, A->R: 17 positions, ...

3. Appliquer le décalage aux lettres du texte clair.

Sans devoir calculer le décalage, on peut utiliser le carré de Vigenère.

Texte clair	t	o	u	t	e	s	t	p	e	r	d	u
Clé	C	R	Y	P	T	O	C	R	Y	P	T	O
Décalage	2	17	24	15	19	14	2	17	24	15	19	14
Texte chiffré	V	F	S	I	X	G	V	G	C	G	W	I

Exercice 4

Déchiffrer le message suivant, chiffré avec le Chiffre de Vigenère, sachant que la clé de chiffrement est informatique:

ARXOD QONDH YXWV

Solution

Pour déterminer le message en clair, il faut compléter le tableau suivant:

1. Noter la clé et le texte chiffré.

2. Compter le décalage de chaque lettre du mot informatique par rapport à la lettre a.

3. Déterminer le texte clair en appliquant le décalage vers la gauche.

Texte clair
Clé	I	N	F	O	R	M	A	T	I	Q	U	E	I	N
Décalage	8	13	5	14	17	12	0	19	8	16	20	4	8	13
Texte chiffré	A	R	X	O	D	Q	O	N	D	H	Y	X	W	V

sesame ouvre toi

Cryptographie symétrique moderne

Les chiffrements vus précédemment sont simples et donc faciles à décrypter, ce qui explique pourquoi ils ne sont plus utilisés aujourd'hui. Les systèmes modernes, comme AES ^{1 1}Advanced Encryption Standard, reposent sur le chiffrement par blocs qui fonctionne plus ou moins de la manière suivante:

1. Remplacer les caractères par un code binaire (par exemple, par l'encodage ASCII), ce qui génère une chaîne de 0 et de 1.

2. Découper cette chaîne en blocs de longueur donnée (par exemple, 128 bits).

3. Pour chaque bloc:

   • Permuter certains bits du bloc selon une table prédéfinie.

   • Chiffrer le bloc en utilisant la clé secrète (par exemple, addition bit par bit).

   • Répéter les deux opérations précédentes plusieurs fois.

Conclusion

Dans un chiffrement symétrique, toute personne connaissant la clé est capable de déchiffrer le texte. Il est donc essentiel de maintenir la clé secrète.

Problèmes:

• La clé doit être transmise par un canal sûr. Comment faire?

• On ne peut pas garantir que l'expéditeur du message est bien celui qu'il prétend être (authentification). Si un intru intercepte la clé, il peut créer des messages frauduleux indétectables (falsification).

---